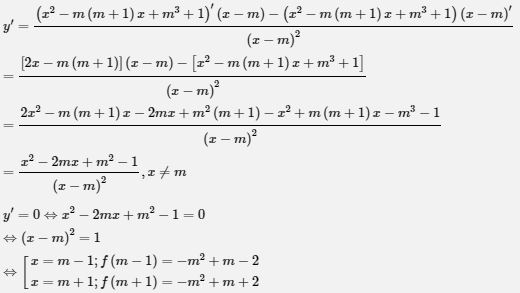Đề bài
Chứng minh rằng với mọi giá trị của \(m\), hàm số: \(y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}\) luôn có cực đại và cực tiểu.
Quảng cáo
Lời giải chi tiết
TXĐ: \(D = {\mathbb{R}}\backslash \left\{ m \right\}\)
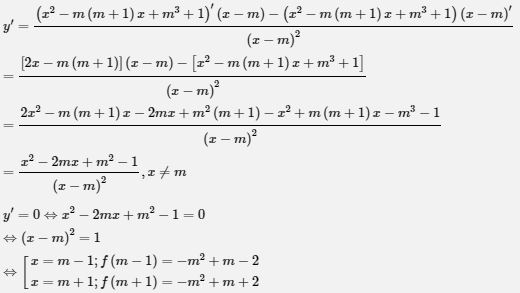
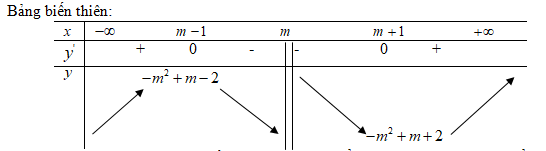
Với mọi giá trị của \(m\), hàm số đạt cực đại tại điểm \(x=m-1\) và đạt cực tiểu tại điểm \(x=m+1\)
Chú ý:
Ta có thể viết lại hàm số f(x) để tính đạo hàm cho đơn giản như sau:
\(\begin{array}{l}
y = \frac{{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1}}{{x - m}}\\
= \frac{{{x^2} - {m^2}x - mx + {m^3} + 1}}{{x - m}}\\
= \frac{{\left( {{x^2} - mx} \right) - \left( {{m^2}x - {m^3}} \right) + 1}}{{x - m}}\\
= \frac{{x\left( {x - m} \right) - {m^2}\left( {x - m} \right) + 1}}{{x - m}}\\
= \frac{{x\left( {x - m} \right)}}{{x - m}} - \frac{{{m^2}\left( {x - m} \right)}}{{x - m}} + \frac{1}{{x - m}}\\
= x - {m^2} + \frac{1}{{x - m}}\\
y' = \left( {x - {m^2} + \frac{1}{{x - m}}} \right)'\\
= 1 - 0 - \frac{1}{{{{\left( {x - m} \right)}^2}}}\\
= 1 - \frac{1}{{{{\left( {x - m} \right)}^2}}}\\
y' = 0 \Leftrightarrow 1 - \frac{1}{{{{\left( {x - m} \right)}^2}}} = 0\\
\Leftrightarrow 1 = \frac{1}{{{{\left( {x - m} \right)}^2}}} \Leftrightarrow {\left( {x - m} \right)^2} = 1\\
\Leftrightarrow \left[ \begin{array}{l}
x - m = 1\\
x - m = - 1
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = m + 1\\
x = m - 1
\end{array} \right.
\end{array}\)
HocTot.Nam.Name.Vn
Chia sẻ
Bình luận
