Bài 11. Thực hành: Đo gia tốc rơi tự do trang 47, 48 Vật Lí 10 Kết nối tri thức

Câu hỏi tr 47

Thảo luận về phương án thí nghiệm dựa trên hoạt động sau: Thả trụ thép rơi qua cổng quang điện trên mảng đứng và trả lời câu hỏi.

Lời giải chi tiết:

1.

Xác định gia tốc rơi tự do của trụ thép theo công thức:

\(g = a = \frac{{2s}}{{{t^2}}}\left( {m/{s^2}} \right)\)

2.

Để xác định gia tốc rơi tự do của trụ thép cần đo đại lượng: quãng đường rơi của trụ thép và thời gian rơi.

3.

Để trụ thép rơi qua cổng quang điện cần chú ý điều chỉnh máng thẳng đứng (quan sát dây rọi) đồng thời điều chỉnh cổng quang điện để trụ thép rơi qua cổng quang điện.

4.

Cần đặt đồng hồ đo thời gian hiện số ở chế độ \(A \leftrightarrow B\) để đo được đại lượng cần đo.

Câu hỏi tr 48

Lời giải chi tiết:

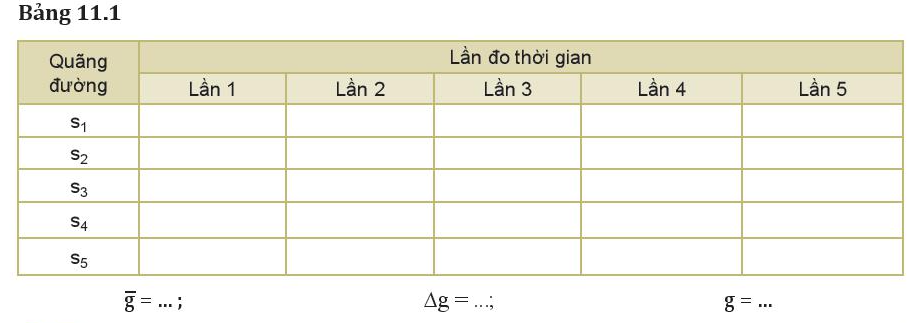
* Kết quả thí nghiệm

Xử lí kết quả với phép đo khi chọn quãng đường s = 0,4 m

1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do

- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)

- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)

- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)

- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)

- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)

Gia tốc trung bình là: \(\overline g  = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)

Sai số tuyệt đối của gia tốc trong các lần đo

\(\begin{array}{l}\Delta {g_1} = \left| {\overline g  - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g  - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g  - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g  - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g  - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)

Sai số tuyệt đối trung bình là: \(\overline {\Delta g}  = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)

Suy ra kết quả: \(g = 9,849 \pm 0,028\)

2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn

- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi

3. Xử lí số liệu và vẽ đồ thị

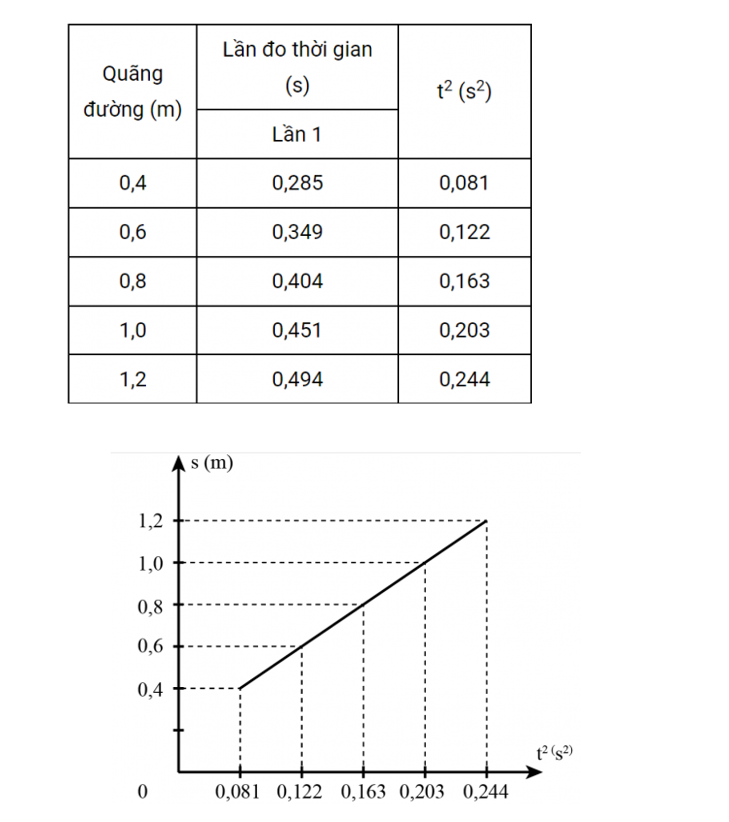4. Đồ thị mô tả mối quan hệ s và t² có dạng một đường thẳng hướng lên, chứng s và t² tỉ lệ thuận với nhau

5. Ta có thể sử dụng hai cổng quang điện để đo thời gian rơi tự do. Khi trụ thép bắt đầu đi vào cổng quang điện thứ nhất thì đồng hồ bắt đầu đo , khi trụ thép đi qua cổng quang điện thứ hai thì đồng hồ kết thúc đo.

Lý thuyết

>> Xem chi tiết: Lý thuyết thực hành: Đo gia tốc rơi tự do - Vật Lí 10