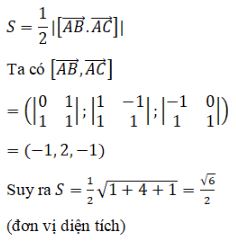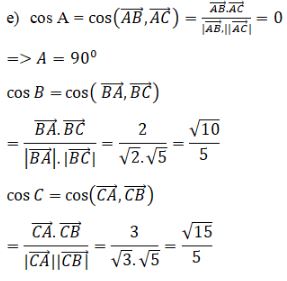Bài 10 trang 81 SGK Hình học 12 Nâng cao

LG a

Chứng minh A, B, C không thẳng hàng.

Phương pháp giải:

Kiểm tra \( \overrightarrow {BA} ,\overrightarrow {BC} \) không cùng phương.

Lời giải chi tiết:

Ta có \(\overrightarrow {BA}  = \left( {1;0; - 1} \right),\overrightarrow {BC}  = \left( {2;1;0} \right)\).
Vì \({1 \over 2} \ne {0 \over 1} \Rightarrow \overrightarrow {BA} ,\overrightarrow {BC} \) không cùng phương do đó A, B, C không thẳng hàng.

LG b

Tính chu vi và diện tích tam giác ABC.

Phương pháp giải:

- Tính độ dài các đoạn thẳng AB, BC, CA suy ra chu vi.

- Chứng minh tam giác ABC vuông suy ra diện tích.

Lời giải chi tiết:

Ta có

\(\eqalign{
& AB = \sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \cr 
& BC = \sqrt {{2^2} + {1^2} + {0^2}} = \sqrt 5 \cr 
& AC = \sqrt {{1^2} + {1^2} + {1^2}} = \sqrt 3 \cr} \)

Vậy chu vi tam giác ABC bằng \(\sqrt 2  + \sqrt 3  + \sqrt 5 \).
Ta có \(B{C^2} = A{B^2} + A{C^2} \Rightarrow \Delta ABC \) vuông tại A nên có diện tích \(S = {1 \over 2}AB.AC = {{\sqrt 6 } \over 2}\)

Chú ý:

Có thể tính diện tích theo công thức như sau:

LG c

Tính độ dài đường cao của tam giác ABC kẻ từ đỉnh A.

Phương pháp giải:

Tính chiều cao theo công thức \({h_a} = \frac{{2S}}{a}\)

Lời giải chi tiết:

Gọi \({h_a}\) là độ dài đường cao kẻ từ A ta có: 
\({S_{ABC}} = {1 \over 2}BC.{h_a} \) \(\Rightarrow {h_a} = {{2{S_{ABC}}} \over {BC}} = {{\sqrt 6 } \over {\sqrt 5 }} = {{\sqrt {30} } \over 5}\)

LG d

Tính các góc của tam giác ABC.

Lời giải chi tiết:

Vì tam giác ABC vuông tại A nên:

\(\cos B = {{AB} \over {BC}} = {{\sqrt 2 } \over {\sqrt 5 }} = {{\sqrt {10} } \over 5}\)

\(\cos C = {{AC} \over {BC}} = {{\sqrt 3 } \over {\sqrt 5 }} = {{\sqrt {15} } \over 5}\)

Chú ý:

Có thể tính cosB, cosC theo công thức:

HocTot.Nam.Name.Vn